
|
| Photo by Alex Knight on Unsplash |
Introduction
The Normal Distribution was first discovered by
Abraham de Moivre
in 1733. Due to historical error it was credited to
Carl Friedrich Guass, who made first reference to the Normal Distribution in 1809 as the
distribution of errors in Astronomy. Since then the distribution was widely
used in various fields and is in continuous development.
The Normal Distribution is the most important continuous probability
distribution and plays a very important role in various statistical analysis. It fits the most of naturally occurring variables like Population Age, Height, Weight, Blood
Pressure, IQ Scores etc. All these follow Normal Distribution when we have
significantly large samples.
Definition
A Continuous Variable "X" is said to follow Normal Distribution with
parameters - Mean (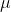 ) and Standard Deviation (
) and Standard Deviation ( ) if it has probability density function:
) if it has probability density function:
Remarks:
- Data distribution under the curve is symmetrical about Mean of the distribution
- Variance tells about how our data is distributed under the curve.
- When we move from Mean to either side of the distribution, the distribution of data decreases rapidly thus making the values at the tails of the curve least significant.
- The tails of the distribution are asymptotic (i.e, the curve continuous to approach but never touches the x-axis)
Properties of Normal Distribution:
- The probability distribution curve is bell shaped and symmetrical about Mean.
- Mean, Median and Mode of the distribution coincide.
- It has zero skewness i.e, it is perfectly symmetrical
- The first and third quartiles are equidistant from median.
- If "X" and "Y" are independent Normal Variates with mean
and
, and variance
and
respectively then their sum (X+Y) is also a Normal Variate with mean (
) and variance (
)
Standard Normal Distribution
Let "X" be a random variable which follows Normal Distribution with Mean (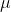 ) and Variance (
) and Variance ( ). The Standard Normal Variable is defined as
). The Standard Normal Variable is defined as  which follows Normal Distribution with Mean 0 (Zero) and Variance 1 (One). The Standard Normal Distribution is given by:
which follows Normal Distribution with Mean 0 (Zero) and Variance 1 (One). The Standard Normal Distribution is given by:
The advantage of Standard Normal Distribution is that it doesn't contain any parameters and enable us to compute area under the normal probability curve.
Z Score for a given value of x can be interpreted as it's (x's) distance from the mean in a Standard Normal Distribution. As we know that the Standard Normal Distribution has mean 0, for a given value of x if Z score is positive then it is Z Score distance from the mean on right side of the curve. If it is negative then it is Z Score distance from the mean on left side of the curve.
Important Findings:
- Z = 1 for a given x value if it is exactly one standard deviation distance from it's mean on the right side i.e, (
+
), and Z = -1 if it lies at one standard deviation distance from it's mean on the left side. i.e, (
-
)
- Z = 2 for a given x value if it is exactly two standard deviation distance from it's mean on the right side i.e, (
+ 2
), and Z = -2 if it lies at two standard deviation distance from it's mean on the left side. i.e, (
- 2
)
- Z = 3 for a given x value if it is exactly three standard deviation distance from it's mean on the right side i.e, (
+ 3
), and Z = -3 if it lies at three standard deviation distance from it's mean on the left side. i.e, (
- 3
)
Area Property of Normal Curve
The area property of normal curve is the building block for decision making in the Hypothesis Testing and also has wide range of applications in various statistical analysis like Operations Research. The total area under the Normal Curve is 1(sum of the probabilities). The curve is also called standard probability curve.
Finding area under the curve between two values (say x = a and x = b) is nothing but we are finding the probability that x lies in between a and b. To find the probability value for x, first standardize it by using  and use the Area Probability Curve Table to find the probability value for the corresponding Z value.
and use the Area Probability Curve Table to find the probability value for the corresponding Z value.
Example:
Q) Students of a class were given an aptitude test. Their marks were found to be normally distributed with mean 60 and standard deviation 5. Find the percentage of students scored
(a)less than 56 marks
(b)between 45 and 65 marks.
Solution for a:
Step 1: Given that mean = 60 and sd = 5, find Z value for a given X value using the above equation.
Z = (56-60)/5 = -0.8
Step 2: After getting the Z - value, use the Area Probability Curve Table to find the corresponding probability(area from  to Z - value).
to Z - value).
For Z = -0.8 the probability value is 0.2119, that is out of 100 students 21 students scored less than 56 marks.
Solution for b:
Step 1: For this we need to find the area lying between x = 45 and x = 65. Find the Z values for both 45 and 65.
Z1 = (45-60)/5 = -3
Z2 = (65-60)/5 = 1
Step 2: Let us first get the area under the higher Z value using the same method as above and say A1 and then the area under the smaller Z value say A2. In order to get area in between we subtract A2 from A1
Here, A1 = 0.8413 and A2 = .0013, area in between Z1 and Z2 = 0.8400, that is out of 100 students 84 students scored between 45 and 65 marks.
Following are the key takeaways from the Area Property of Normal Distribution:
- The area under the curve in between the interval of one standard deviation from the mean on either sides of curve i.e (
-
,
+
) or [Z = -1, Z = +1] is found to be 0.6826. This says that 68.26% of the data lies in the range of one standard deviation from the mean on both sides.
- The area under the curve in between the interval of two standard deviation from the mean on either sides of curve i.e (
- 2
,
+ 2
) or [Z = -2, Z = +2] is found to be 0.9544. This says that 95.44% of the data lies in the range of two standard deviations from the mean on both sides.
- The area under the curve in between the interval of three standard deviation from the mean on either sides of curve i.e (
- 3
,
+ 3
) or [Z = -3, Z = +3] is found to be 0.9973. This says that 99.73% of the data lies in the range of three standard deviations from the mean on both sides.
- 50% of the data in the distribution lies in between the 0.745 standard deviations from the mean on both sides i.e, (
- 0.745
,
+ 0.745
)
- 95% of the data in the distribution lies in between the 1.96 standard deviations from the mean on both sides i.e, (
- 1.96
,
+ 1.96
)
- 99% of the data in the distribution lies in between the 2.58 standard deviations from the mean on both sides i.e, (
- 2.58
,
+ 2.58
)
Better Understanding of Area Property, Z Values/Scores and Area Under the curve is so important for understanding basic concepts in Hypothesis Testing like Test Statistic, Confidence Intervals, p-values which we will discuss in next blog post.
Importance of Normal Distribution:
- Most of the distributions that we use in general like Binomial, Poisson. etc can be approximated by the Normal Distribution. (For infinitely large value for n in the Binomial and for infinitely large value for Poisson parameter m both results in Normal Distribution)
- The entire theory of Small Sample tests viz, t, F and Chi-Squared tests is based on the fundamental assumption that the parent population from which the samples are drawn follow a Normal Distribution.
- The distributions of t, F and Chi-Squared tends to Normal for large samples.
- Even if a Variable is not Normally distributed i.e if it is skewed, it can be brought to normal form by applying transformations to the variable. (refer to previous blog on Skewness)
Central Limit Theorem
Central Limit Theorem states that if we have a population with mean (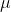 ) and standard deviation(
) and standard deviation( ) and take a sufficiently large number of random samples with replacement, then the distribution of the means of those random samples will approximate to Normal Distribution.
) and take a sufficiently large number of random samples with replacement, then the distribution of the means of those random samples will approximate to Normal Distribution.
When I first read the theorem statement, I thought of testing it practically and had done it. I took 1000 random numbers from the range of (-10,000, +10,000) and computed the mean of those 1000 numbers. This is repeated for a given n number of times in a function and plotted those n means.
The Result: As we increase n value, the approximation to normal distribution also increases.
See you in the next blog post. Keep Smiling. Keep Learning. Have a great day.




Amazing write up Uday. Explained very well.
ReplyDeleteThank You.
DeleteKeep Reading. Keep Supporting.
It was awesome. Easy to understand... It's very helpful for reader's ....
ReplyDeleteThank you so much Ansh!
DeleteKeep Reading. Keep Supporting.
Very good explanation
ReplyDeleteThank you Deepika.
DeleteKeep reading. Keep supporting.