Hypothesis Testing - Standard Error, Level of Significance, p-value and Critical Values.

 

Image by Gerd Altmann from Pixabay

"In Statistics we study the Chances or Probabilities of Occurrence or Happening of an Event or Phenomenon. In the world of Statistical Analysis presenting the results with 100% strong evident is impossible"  

Introduction

In general gaining the information regarding the characteristics of whole population is practically not possible. It incurs a lot of money, time, labor and other constraints. So we take a sample from the population, study about it's characteristics and try to draw conclusions or to estimate the population characteristics from it. For example, A doctor records the Blood Pressure(BP) readings of 100 patients suffering with Hypertension and computes the average(Sample average) of those readings. Doctor uses this sample average information to draw conclusion about the average Blood Pressure (Population average) of whole patients who are suffering from Hypertension.

Parameter and Statistic

The Statistical characteristics of the population such as Mean(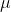), Variance(σ²), Correlation Coefficient(ρ) are called Parameters.

The Statistical characteristics which are computed from the samples corresponding to Population Parameters like Mean (x̅), Variance(s²) and sample correlation coefficient(r) are called Statistic.

Parameters are the functions of the population values while Statistic are functions of the sample observations. In general, population parameters are estimated from the sample statistic.

Sample Distribution

Consider we have a population with N values. Let us take a random sample of size n from this population and compute the sample statistic (let it be Mean or Variance or Correlation Coefficient). We do this for all the different possible samples that we can draw from the Population. The distribution of thus computed sample statistic's from all the possible samples that we draw from the population is called Sample Distribution. 

Example:

Consider the above case of a Doctor taking the sample of 100 Hypertension patients for computing the sample average BP. Now consider he has the population of 1000 patients, he has to consider all the possible samples from the population, i.e, samples, say it's value is k and compute the mean of these k samples to form a distribution with those means. Then such formed distribution with sample averages is called Sample Distribution of Mean.  

Standard Error (S.E)

The Standard Deviation of the Sampling Distribution of a statistic is known as it's Standard Error. If we compute Standard Deviation of the Sample Distribution of mean then it is called Standard Error of Mean. Based on Standard Error we can say how well a sample will represent the whole population. The smaller the Standard Error, the more it will represent the whole population and vice versa. The larger the sample size n the smaller the Standard Error. As we keep increasing the sample size obviously the sample will lead to the whole population, which in turn represents the whole population thus we will have smaller Standard Error. 

Standard Error of sample mean is given by:

  

Hypothesis

Hypothesis is a set of assumptions that are made about the population parameter after analyzing the sample statistic. Every hypothesis testing starts with these set of assumptions and test for possible acceptance or rejections. The conventional way to testing hypothesis is to construct two exclusive assumptions. So that one of these is accepted, other one is rejected and vice versa. 

Null Hypothesis: Null Hypothesis is the Hypothesis which is tested for possible rejection under the assumption that it is true. Denoted by

Alternative Hypothesis: Alternative Hypothesis is the Hypothesis which is complementary (exclusive) of Null Hypothesis. Denoted by

Example: Let us consider the above said Blood Pressure example, Doctor has the computed average Blood Pressure readings of 100 Hypertension patients, say the average is: 135/85 mm of Hg. Now he wants to test whether the sample average is same as the population average. In order to test the hypothesis he forms the Null and Alternative Hypothesis as below:

Null Hypothesis (): Population Average BP is equal to Sample Average. 

i.e, .

Alternative Hypothesis(): Population Average BP is not equal to Sample Average.

i.e, .

One Tailed and Two Tailed test

When we are performing a hypothesis test, if the alternative hypothesis is directed to only one side then we say that test is One Tailed test (left tailed or right tailed).

Example: In the above example, if the doctor's alternative hypothesis is like, Population Average BP is greater than the Sample Average i.e, 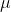> 135/85 mm of Hg then it is a Right -  Tailed test or Population Average BP is less than the Sample Average i.e, 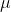< 135/85 mm of Hg then it is a Left - Tailed test.    

Before proceeding to test our Hypothesis, we need to first determine the percentage of error that we could allow in our testing procedure. (As I said in the beginning, In the world of statistical analysis we cannot present our results with 100% evident or confident or significant) 

Level of Significance

In the Hypothesis testing, the maximum probability with which one is willing to take risk or allowing error to occur is called Level of Significance. It is denoted by 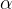and should be determined before we begin the testing procedure. We usually allow a 5% error (probability of 0.05) or 1% error (probability of 0.01)  in our tests i.e, Level of Significance = 0.05 or 0.01. For Example, if we incorporate 5% level of significance in testing our hypothesis, then there are about 5 chances in 100 that we would reject our Null Hypothesis when it should be accepted(that's what an error is!). We are about 95% confident that we made a right decision through our test. In such a case say that the hypothesis has been rejected at 5% level of significance which means that we could be wrong with probability of 0.05. 

When we test our Null Hypothesis for possible rejection with 5% level of significance, then we are allowing a 5% error in our test. This 5% chance of error is distributed equally at both the tails in the case of two tailed test i.e, 2.5%(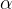/2) at the left tail and 2.5%(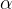/2) at the right tail. In case of One Tailed test, the chance of error is totally on the side of the tail on which we are testing i.e, chance of error is on the right tail for the Right - Tailed test and on left tail for the Left - Tailed test.

 

Test Statistic

Till now we have seen building the conditions for testing our Hypothesis. Finding the Test Statistic is the first step towards the decision making procedure. For large samples the Standard Normal Variate corresponding to the statistic x , the Test Statistic Z is given by:

where, E(x) is the mean of the sampling distribution of the statistic

S.E(x) is the standard deviation of the sampling distribution of the statistic.

Example: Consider the above example where doctor is testing the Null Hypothesis (:  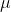= 135/85 mm of Hg), here E(x) is the mean of all the possible sample(say, k) means and S.E(x) is the standard deviation of all the possible sample(say, k) means. 

p-value

Under the Standard Normal Distribution of sampling distribution of mean (statistic) the p-value represents the area under the curve for the corresponding Z - value computed from the test statistic. Under the two tail test people often get confused while finding the area under the curve, should we consider the area from the left tail to the computed Z value or from the right tail to the computed Z value. We always find area under the curve from the right tail to the computed Z - Value because we have a modulus function in Test Statistic which makes sure all the computed Z - values to lie on the right side of the curve. 

Critical Value

The value of the test statistic which separates the Standard Normal Curve into Critical (Rejection) region and Acceptance region is called Critical Value. If the computed test statistic Z falls in Critical region then we reject our Null Hypothesis and if it falls in Acceptance region we accept our Null Hypothesis. Critical value depends on:

1. Level of significance

2. Alternative Hypothesis, whether it is one tailed or two tailed test. 

The critical value of the test statistic at the level of significance (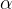) for a two-tailed test is given by i.e, the value of Z for a p-value of 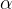/2 and for one-tailed test is given by i.e, the value of Z for a p-value of .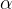 

Example:

Suppose we are testing a Hypothesis with a level of significance 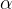 = 0.05 and it is a two tailed test then the critical value for test statistic is the value of Z when p = 0.025 i.e, Z = 1.96.

NOTE: Critical Values are constant for a given level of significance (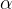) and type of test (two tailed or one tailed).

• For  = 0.05 and two tailed test, Z = 1.96 (p = 0.025)
• For  = 0.05 and one tailed test, Z = 1.645 (p = 0.05)
• For  = 0.01 and two tailed test, Z = 2.58 (p = 0.005)
• For  = 0.01 and one tailed test, Z = 2.33 (p = 0.01)

Check for more Z values and it's corresponding p-values.

Two Tailed test

Right Tailed test

Left Tailed test

If we observe the graph we can say that as Z increases it's corresponding p-value(area under the curve) decreases. In order to reject our Null Hypothesis we should have a very high Z Score which corresponds to very less p-value or if we want to accept our Null Hypothesis we should have very less Z Score, which corresponds to very high p-value. 

Test Procedure:

Step 1: Setting up the Null Hypothesis .

Step 2: Set up the Alternate Hypothesis , which is complementary to  which will indicate our test is whether one-tailed or two-tailed.

Step 3: Choose the appropriate Level of Significance. 

Step 4: Compute the Test Statistic .

Step 5: Inference: We compare the computed test statistic Z with the critical value of test statistic  

• If , we reject our Null Hypothesis  at  % level of significance. 
• If  , we accept our Null Hypothesis  at  % level of significance and reject our Alternative Hypothesis .